TEOREMA Siano  f: A ® B e g: B ® C  due funzioni biunivoche.La funzione h = gof : A ® C è biunivoca.

Diamo la dimostrazione
Dobbiamo dimostrare che se f e g sono sia iniettive che suriettive , allora h = gof è sia iniettiva che suriettiva.
1) Poichè f è iniettiva ,  .
Poichè g è iniettiva , .
Quindi  e perciò h è iniettiva.
2) Sia z un qualunque elemento dell'insieme C. Poichè g è suriettiva, esiste un   tale che .
Ma f è suriettiva, dunque esiste un tale  che .
Quindi .
Perciò per qualsiasi elemento ,   esiste tale che  e quindi h è suriettiva.

La dimostrazione appena affrontata ci permette di affermare che :
componendo due funzioni iniettive si ottiene una funzione iniettiva
componendo due funzioni suriettive si ottiene una funzione suriettiva

 Per una revisione dei concetti di funzione suriettiva, iniettiva, biunivoca o biettiva  puoi consultare l'Elemento 8.


Esempi

1) Dati gli insiemi

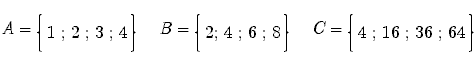
e le funzioni



f, g e h sono biunivoche, come si può facilmente dedurre dai diagrammi che seguono




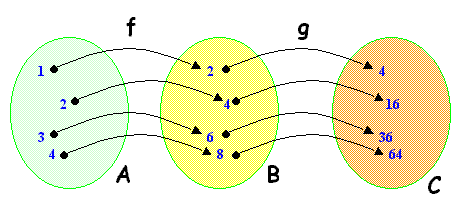
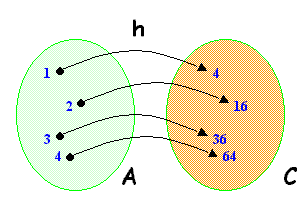
Ti ricordo che quando una funzione è biunivoca ad ogni elemento del suo dominio corrisponde uno ed un solo elemento del suo codominio e viceversa: in altre parole esiste una corrispondenza "uno a uno" fra gli elementi del dominio e quelli del codominio.
Analizzando la rappresentazione sagittale di una funzione biunivoca, si osserva che ad ogni elemento del codominio arriva una ed una sola freccia: è quello che si verifica per le funzioni f, g e h del nostro esempio.

2) Siano A  l'insieme  degli studenti di una classe presenti ad una verifica, B l'insieme dei numeri di registro degli studenti in questione,  C  l'insieme delle verifiche svolte dagli studenti in questione in una certa data . Definiamo le seguenti funzioni :
f: A ® B   f associa ad ogni studente  x il numero di registro  y = f(x)  
g: B ® C   g associa al numero di registro y = f(x) la corripondente verifica  t = g(y) = g(f(x))
Consideriamo  la funzione h = gof : A ® C ; h associa ad ogni studente la sua verifica.
f è biunivoca in quanto ogni numero di registro y = f(x)  è immagine di uno ed un solo studente .
g è biunivoca in quanto ogni verifica è immagine di uno ed un solo numero di registro.
h   è biunivoca per il teorema precedente dimostrato ; comunque è facile verificare che h  è biunivoca anche utilizzando la definizione di funzione biunivoca. Infatti , basta osservare che ogni verifica t = h(x) appartiene ad uno ed un solo studente x cioè ogni elemento dell'insieme C è immagine di uno ed un solo elemento dell'insieme A.


Attività 1
Siano  A l'insieme  dei comuni italiani, B l'insieme delle province italiane e C l'insieme delle regioni . Consideriamo le seguenti funzioni:
f: A ® B   f associa ad ogni comune x la provincia y=f(x) in cui tale comune si trova
g: B ® C   g associa alla provincia y = f(x) la regione  t = g(y) = g(f(x)) in cui tale provincia si trova.
Considera la funzione h = gof : A ® C ; h associa ad ogni comune x la regione h(x) = t = g(y) = g(f(x)) in cui tale comune si trova.
h è biunivoca ? Motiva la risposta.
Invia soluzioni ed eventuali osservazioni alla conference Sir2_MatFunzEL11Quaderno.


Attività 2
Siano N l'insieme dei numeri naturali, P l'insieme dei numeri pari e D l'insieme dei numeri dispari.
Considera le funzioni  f e g così definite :
f: N ® P , f associa ad ogni numero naturale il suo doppio
g: P ® D ,  g associa ad ogni numero naturale il suo successivo
Considera la funzione h = gof.
 quali sono il dominio ed il codominio di h ?
 qual è l'immagine di 0.5 in h ?
 h  è biunivoca? Motiva la risposta.
Invia soluzioni ed eventuali osservazioni alla conference Sir2_MatFunzEL11Quaderno.


Attività 3
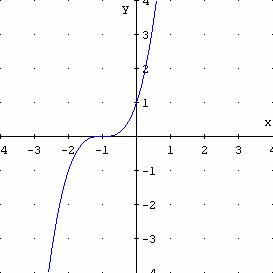
Considera la funzione

Osserva il suo grafico cartesiano.

utilizza il grafico per dimostrare che h è biunivoca
trova due funzioni f e g biunivoche che, composte, diano come risultato h.
Invia soluzioni ed eventuali osservazioni alla conference Sir2_MatFunzEL11Quaderno.


Attività 4
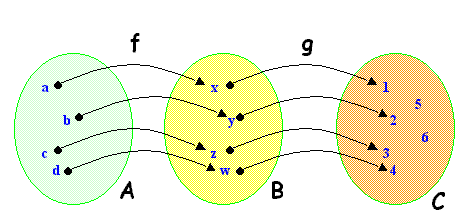
Siano f: A ® B e g: B ® C le due funzioni rappresentate in figura mediante il loro diagramma sagittale.

rappresenta mediante un diagramma sagittale la funzione h = gof
precisa dominio e codominio di h
h è biunivoca ? Motiva la risposta.
Invia soluzioni ed eventuali osservazioni alla conference Sir2_MatFunzEL11Quaderno.

Attività 5
Clicca qui e potrai svolgere  un test on line sui concetti che hai imparato.




Approfondimento facoltativo
Analizza le funzioni composte che hai incontrato negli esempi e nelle attività delle lezioni precedenti. Quali tra queste sono biunivoche ? Ricordati di motivare brevemente le risposte.
Invia soluzioni ed eventuali osservazioni alla conference